设函数![]() .
.
25.讨论![]() 的单调性;
的单调性;
26.证明当![]() 时,
时,![]() ;
;
27.设![]() ,证明当
,证明当![]() 时,
时,![]() .
.
(Ⅰ)答案
(Ⅰ)当![]() 时,
时,![]() 单调递增;当
单调递增;当![]() 时,
时,![]() 单调递减;
单调递减;
解析
(I)由题设,![]() 的定义域为
的定义域为![]() ,
,![]() ,令
,令![]() ,解得
,解得![]()
当![]() 时,
时,![]() ,
,![]() 单调递增;当
单调递增;当![]() 时,
时,![]() ,
,![]() 单调递减
单调递减
考查方向
本题主要考查利用导数研究函数的单调性和不等式的证明与解法等知识,为高考题的必考题,在近几年的各省高考题出现的频率较高
解题思路
(I)首先求出导函数![]() ,然后通过解不等式
,然后通过解不等式![]() 或
或![]() 可确定函数
可确定函数![]() 的单调性
的单调性
件优网498b司学97cc0250有广公升东方途-技慧元科限软易错点
对利用导数研究函数的单调性和不等式的证明与解法理解出现错误、计算错误
(Ⅱ)答案
(Ⅱ)(II)由(I)知,![]() 在
在![]() 处取得最大值,最大值为
处取得最大值,最大值为![]() ,所以当
,所以当![]() 时,
时,![]() ,故当
,故当![]() 时
时![]() ,即
,即![]() 。
。
解析
(II)由(I)知,![]() 在
在![]() 处取得最大值,最大值为
处取得最大值,最大值为![]() ,所以当
,所以当![]() 时,
时,![]() ,故当
,故当![]() 时
时![]() ,即
,即![]() 。
。
考查方向
本题主要考查利用导数研究函数的单调性和不等式的证明与解法等知识,为高考题的必考题,在近几年的各省高考题出现的频率较高
解题思路
(II)左端等式可利用(I)的结论证明,右端将左端的![]() 换为
换为![]() 即可证明;
即可证明;
易错点
对利用导数研究函数的单调性和不等式的证明与解法理解出现错误、计算错误
(Ⅲ)答案
(Ⅲ)(III)由题设![]() ,
,![]() ,则
,则![]() ,令
,令![]() 解得
解得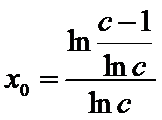 ;当
;当![]() ,
,![]() 单调递增,当
单调递增,当![]() ,
,![]() ,
,![]() 单调递减,由(II)知,
单调递减,由(II)知,![]() ,故
,故![]() ,又
,又![]() ,故当
,故当![]()
时,![]() ,所以当
,所以当![]() 时,
时,![]()
解析
(III)由题设![]() ,
,![]() ,则
,则![]() ,令
,令![]() 解得
解得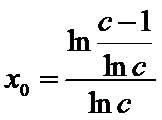 ;当
;当![]() ,
,![]()
单调递增,当![]() ,
,![]() ,
,![]() 单调递减,由(II)知,
单调递减,由(II)知,![]() ,故
,故![]() ,又
,又![]() ,故当
,故当![]() 时,
时,![]() ,所以当
,所以当![]() 时,
时,![]()
慧元优方件限有9fb0477d-916baf91秀技点司网498b公6552东方学97cc0250科心升得途软量44279740广考查方向
本题主要考查利用导数研究函数的单调性和不等式的证明与解法等知识,为高考题的必考题,在近几年的各省高考题出现的频率较高
解题思路
变形所证不等式构造新函数,然后通过利用导数研究函数的单调性来处理
易错点
对利用导数研究函数的单调性和不等式的证明与解法理解出现错误、计算错误
考察知识点
函数性质的综合应用