（
2017年高考全国II卷
）
学94928724点限软量慧2115bc0a东元根科件优的公技d66aae9a量-网升费962b广有途司
设O为坐标原点，动点M在椭圆C：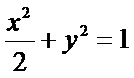
上，过M作x轴的垂线，垂足为N，点P满足
.
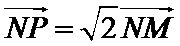20.(12分)
上，过M作x轴的垂线，垂足为N，点P满足.
(1)求点P的轨迹方程;
(2)设点
在直线
上，且
.证明：过点P且垂直于OQ的直线
过C的左焦点F.
答案
(1)
(2)见解析
解析
(1)设
由
知
即
又
点在椭圆
上，则有
即
-上量广cdfc途优的慧2115bc0a技d66aae9a量48df90b5科公75f7是2ac64004限司东费学94928724点升费962b径件元根4798软量d45a网得有
(2)设
，则有
即
设椭圆右焦点
又
∴
∴过点
且垂直于
的直线
过
的左焦点
.
考查方向
(1)直接法求轨迹方程;(2)圆锥曲线的定点、定值问题
科元根4798-上量公75f7是2ac64004技d66aae9a量48df90b5731c75ee学94928724点1a50途升费962b径上网得方有慧2115bc0a限件优的广cdfc东费软量d45ab2e2司
解题思路
(1)设所求动点坐标及相应已知动点坐标，利用条件列两种坐标关系，最后代入已知动点轨迹方程，化简可得所求轨迹方程，(2)设
，由题意
得出
，再
=0，所以
，得出结论.
易错点
直线过定点问题