(
2017年高考全国I卷
)
件e923网公东4a19软广有0985方科西学智司限升途-慧技优元
已知函数![]() ,
,![]() .
.
(1)当![]() 时,求不等式
时,求不等式![]() 的解集;
的解集;
(2)若不等式![]() 的解集包含[–1,1],求
的解集包含[–1,1],求![]() 的取值范围.
的取值范围.
答案
(1)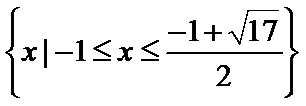 (2)
(2)![]()
解析
(1)当a=1时,不等式![]() 等价于
等价于![]() ①
①
当![]() 时,①式化为
时,①式化为![]() ,无解;
,无解;
当![]() 时,①式化为
时,①式化为![]() ,从而
,从而![]() ;
;
当![]() 时,①式化为
时,①式化为![]() ,从而
,从而![]() ,
,
所以![]() 的解集为
的解集为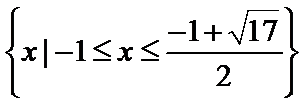
(2)当![]() 时,
时,![]() .
.
所以![]() 的解集包含
的解集包含![]() ,等价于当
,等价于当![]() 时
时![]() .
.
又![]() 在
在![]() 的最小值必为
的最小值必为![]() 与
与![]() 之一,所以
之一,所以![]() 且
且![]() ,得
,得![]() .
.
所以![]() 的取值范围为
的取值范围为![]() .
.
考查方向
本题考查绝对值不等式的解法,去掉绝对值符号是关键,考查分类讨论思想与等价转化思想的综合运用,属于中档题.
解题思路
(1)当a=1时,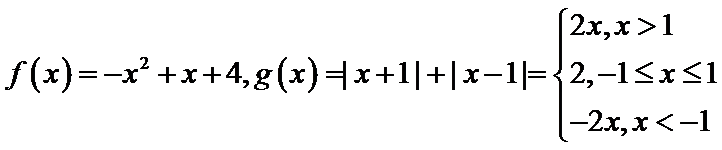 ,分
,分![]() 三类讨论,结合g(x)与f(x)的单调性质即可求得
三类讨论,结合g(x)与f(x)的单调性质即可求得![]() 的解集为
的解集为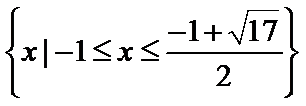 ;
;
(2)依题意得:![]() 在[-1,1]恒成立?
在[-1,1]恒成立?![]() 在[-1,1]恒成立,只需
在[-1,1]恒成立,只需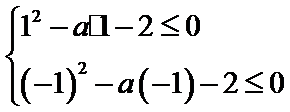 ,解之即可得a的取值范围.
,解之即可得a的取值范围.
易错点
解含有绝对值的不等式的关键是把含有绝对值的不等式转化为不含绝对值符号的不等式,然后再求解,但这种转化必须是等价转化,尤其是平方法去掉绝对值符号时,一定要注意两边非负这一条件,否则就会扩大或缩小解集的范围.