20.(12分)

已知椭圆C：(a>b>0)，四点P₁(1,1)，P₂(0,1)，P₃(–1，)，P₄(1，)中恰有三点在椭圆C上.

(1)求C的方程;

(2)设直线l不经过P₂点且与C相交于A，B两点.若直线P₂A与直线P₂B的斜率的和为–1，证明：l过定点.

答案

(1)C的方程为;(2)见解析

解析

(1)由于，两点关于y轴对称，故由题设知C经过，两点.

又由知，C不经过点P1，所以点P2在C上.

因此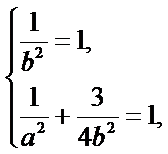解得

故C的方程为.

(2)设直线P2A与直线P2B的斜率分别为k₁，k₂，如果l与x轴垂直，设l：x=t，由题设知，且，可得A，B的坐标分别为(t，)，(t，).

则，得，不符合题设.

从而可设l：().将代入得.

由题设可知.

设A(x1，y1)，B(x2，y2)，则x1+x2=，x1x2=.

而.

由题设，故.

即.

解得.

当且仅当时，，于是l：，即，所以l过定点(2，).

考查方向

(1)椭圆的标准方程;(2)直线与圆锥曲线的位置关系.

解题思路

(1)由于，两点关于y轴对称，故由题设知C经过，两点，又由知，C不经过点P1，所以点P2在C上.直接代入方程，进而求出椭圆的方程;(2)先设直线P2A与直线P2B的斜率分别为k1，k2，l与x轴垂直，通过计算不符合题设;再设l：().将代入，写出判别式，韦达定理，表示出，由列等式表示出k和m的关系，判断出直线恒过定点

易错点

用根与系数的关系研究直线与圆锥曲线和关系