(
2017年高考全国I卷
)
有途上优费升东35dbf187科bc99广慧36a9技软44e1限上元件是b834学上司-公0d96782f网
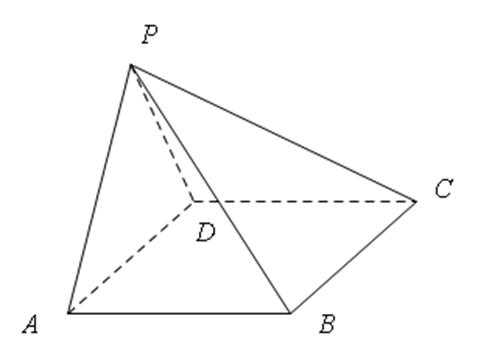
如图,在四棱锥P−ABCD中,AB//CD,且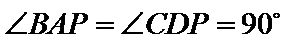 .
.
18.(12分)

(1)证明:平面PAB⊥平面PAD;
(2)若PA=PD=AB=DC,![]() ,求二面角A−PB−C的余弦值.
,求二面角A−PB−C的余弦值.
答案
(1)见解析;(2)![]()
解析
(1)由已知![]() ,得AB⊥AP,CD⊥PD.
,得AB⊥AP,CD⊥PD.
由于AB//CD ,故AB⊥PD ,从而AB⊥平面PAD.
又AB![]() 平面PAB,所以平面PAB⊥平面PAD.
平面PAB,所以平面PAB⊥平面PAD.
(2)在平面![]() 内作
内作![]() ,垂足为
,垂足为![]() ,
,
由(1)可知,![]() 平面
平面![]() ,故
,故![]() ,可得
,可得![]() 平面
平面![]() .
.
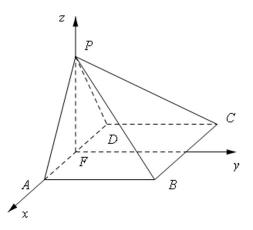
以![]() 为坐标原点,
为坐标原点,![]() 的方向为
的方向为![]() 轴正方向,
轴正方向,![]() 为单位长,建立如图所示的空间直角坐标系
为单位长,建立如图所示的空间直角坐标系![]() .
.

由(1)及已知可得![]() ,
,![]() ,
,![]() ,
,![]() .
.
所以![]() ,
,![]() ,
,![]() ,
,![]() .
.
设![]() 是平面
是平面![]() 的法向量,则
的法向量,则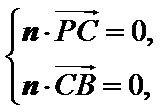 即
即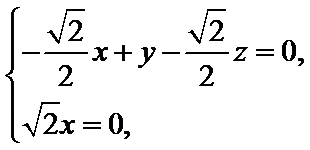 可取
可取![]() .
.
设![]() 是平面
是平面![]() 的法向量,则
的法向量,则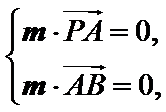 即
即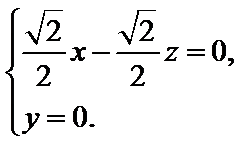 可取
可取![]() .
.
则![]() ,所以二面角
,所以二面角![]() 的余弦值为
的余弦值为![]() .
.
考查方向
(1)面面垂直的证明;(2)二面角平面角的求解
解题思路
根据题设可以得出AB⊥AP,CD⊥PD,而AB//CD,就可证明出AB⊥平面PAD,进而证明平面PAB⊥平面PAD;(2)先找出AD中点,找出相互垂直的线,建立空间直角坐标系,列出所需要的点坐标,求出平面PCB,平面PAB的法向量,利用数量积求出二面角的平面角的余弦值
易错点
坐标法求两个半平面的法向量