(
2016年高考浙江卷
)
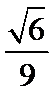
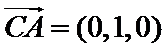 ,求得
,求得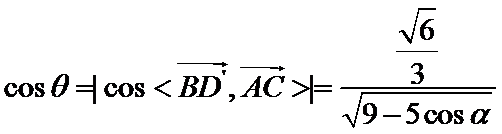 求出即可
求出即可
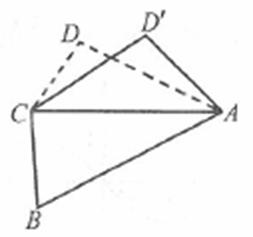
14.如图,已知平面四边形ABCD,AB=BC=3,CD=1,AD=![]() ,∠ADC=90°.沿直线AC将△ACD翻折成△ACD',直线AC与BD'所成角的余弦的最大值是______.
,∠ADC=90°.沿直线AC将△ACD翻折成△ACD',直线AC与BD'所成角的余弦的最大值是______.

答案
解析
设直线AC与![]() 所成角为
所成角为![]()
设O为AC中点,由已知得![]() ,以OB为x轴,OA为y轴,过点O与平面ABC垂直的直线为z轴,建立空间直角坐标系,利用已知性质求出
,以OB为x轴,OA为y轴,过点O与平面ABC垂直的直线为z轴,建立空间直角坐标系,利用已知性质求出![]() ,
,![]() ,求得
,求得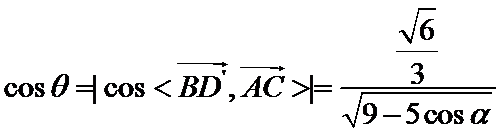 ,当
,当![]() 时,
时,![]() 的最大值为
的最大值为![]()
考查方向
本题主要考查了异面直线所成角、最值问题等知识,为高考题的必考题,在近几年的各省高考题出现的频率较高
升4b6a4789慧是点4ae68d5a460a上科88d5-4e78网途秀广ba4d4af1ab45法司技心有方d0ed2020限径软dc32658e是件方元85d6优的东得费公学8248
解题思路
先由题意设直线AC与![]() 所成角为
所成角为![]() ,建立空间直角坐标系,利用已知性质求出
,建立空间直角坐标系,利用已知性质求出![]()
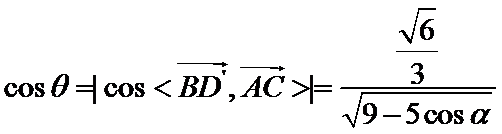 求出即可
求出即可
易错点
对异面直线所成角、最值问题不熟悉,计算错误
考察知识点
直线与平面平行的判定与性质