已知椭圆E：
的两个焦点与短轴的一个端点是直角三角形的三个顶点，直线l:y=-x+3与椭圆E有且只有一个公共点T.
（I）求椭圆E的方程及点T的坐标;
（II）设O是坐标原点，直线l’平行于OT,与椭圆E交于不同的两点A、B，且与直线l交于点P.证明：存在常数λ，使得∣PT∣2=λ∣PA∣·∣PB∣，并求λ的值.
(Ⅰ)答案
，点T坐标为(2,1);
解析
(I)设短轴一端点为
，左，右焦点分别为
，
则
.
由题意，
为直角三角形.
∴
解得
，
∴
.
代入
可得
.
与椭圆
只有一个交点，则
，解得
.
∴
.
由
，解得
，则
，所以
的坐标为
。
考查方向
本题考查椭圆的标准方程及其几何性质，考查学生的分析问题解决问题的能力和数形结合的思想.
解题思路
本题考查椭圆的标准方程及其几何性质，考查学生的分析问题解决问题的能力和数形结合的思想.在涉及到直线与椭圆(圆锥曲线)的交点问题时，一般都设交点坐标为
，同时把直线方程与椭圆方程联立，消元后，可得
，再把
用
表示出来，并代入刚才的
，这种方法是解析几何中的“设而不求”法.可减少计算量，简化解题过程.
易错点
本题考查椭圆的标准方程及其几何性质，考查学生的分析问题解决问题的能力和数形结合的思想.易在第二问运算中出错。
(Ⅱ)答案
.
解析
(II)设
在
上，由
，
平行
.
得
的参数方程为
代入椭圆
得.
.
整理可得
.
设两根为
，
则有
.
而
，
，
.
故有
.
由题意
.
∴
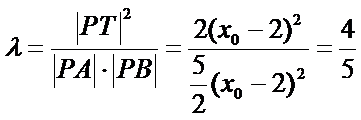， 故存在这样的
.
考查方向
本题考查椭圆的标准方程及其几何性质，考查学生的分析问题解决问题的能力和数形结合的思想.
解题思路
本题考查椭圆的标准方程及其几何性质，考查学生的分析问题解决问题的能力和数形结合的思想.在涉及到直线与椭圆(圆锥曲线)的交点问题时，一般都设交点坐标为
，同时把直线方程与椭圆方程联立，消元后，可得
，再把
用
表示出来，并代入刚才的
，这种方法是解析几何中的“设而不求”法.可减少计算量，简化解题过程.
易错点
本题考查椭圆的标准方程及其几何性质，考查学生的分析问题解决问题的能力和数形结合的思想.易在第二问运算中出错。
考察知识点
椭圆的定义及标准方程