17. 记S_n为等比数列的前n项和，已知S₂=2，S₃=?6.

(1)求的通项公式;

(2)求S_n，并判断S_n+1，S_n，S_n+2是否成等差数列.

答案

(1);(2)见解析

解析

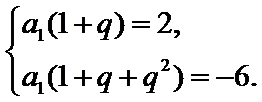(1)设的公比为.由题设可得解得，.

故的通项公式为.

(2)由(1)可得.

由于，

故，，成等差数列.

考查方向

本题考查等比数列通项公式，等比数列前n项和，等差数列的性质，考查计算能力，属于中档题.

解题思路

(1)由题意可知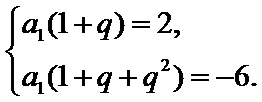，列方程即可求得q及，根据等比数列通项公式，即可求得的通项公式;

(2)由(1)可知.利用等比数列前n项和公式，即可求得，分别求得，显然，则，，成等差数列.

易错点

等差、等比数列各自有一些重要公式和性质(略)，这些公式和性质是解题的根本，用错了公式和性质，自然就失去了方向。解决这类问题的一个基本出发点就是考虑问题要全面，把各种可能性都考虑进去，认为正确的命题给予证明，认为不正确的命题举出反例予以说明

网0f99cf7a广软b6d9司东慧公升优限智技件科途有法学元fd1c0c07-