(
2017年高考全国III卷
)
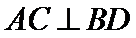 ;
;
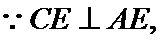 ,
,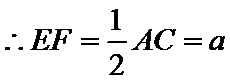 ,
, 在直角
在直角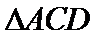 中,
中,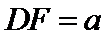 ,
,
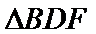 中有
中有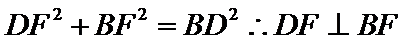 ,又
,又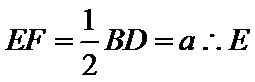 为
为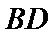 中点,
中点,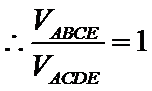
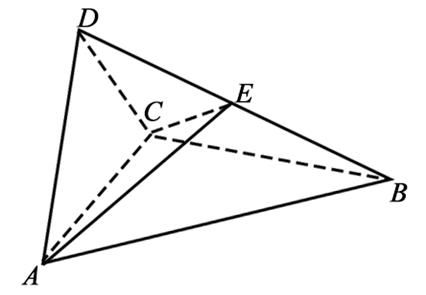
19.(12分)如图,四面体![]() 中,
中,![]() 是正三角形,
是正三角形,![]()
网广b3cb件东软限智9a57元途升有优技科2f343cab司慧公心-学
(1)证明:
(2)已知![]() 是直角三角形,
是直角三角形,![]() ,若
,若![]() 为棱
为棱![]() 上与
上与![]() 不重合的点,且
不重合的点,且![]() ,求四面体
,求四面体![]() 与四面体
与四面体![]() 的体积比.
的体积比.

答案
(1)见解析 (2)1
广b3cb西途网c3c1方优件有软费元东技bf3c慧司科2f343cab升限智9a57公心48af-学解析
(1)证明:取![]() 中点
中点![]() ,连
,连![]() ,∵
,∵![]() ,
,![]() 为
为![]() 中点,
中点,
∴![]() ,又∵
,又∵![]() 是等边三角形,∴
是等边三角形,∴![]() ,
,
又∵![]() ,∴
,∴![]() 平面
平面![]() ,
,![]() 平面
平面![]() ,∴
,∴![]() .
.
(2)由题意,令![]() ,取
,取![]() 中点
中点![]() ,即
,即![]() ,
,
考查方向
(1)线面垂直的判定定理;(2)四面体的体积
解题思路
(1)由![]() ,又
,又![]() 是等边三角形,∴
是等边三角形,∴![]() ,∴
,∴![]() 平面
平面![]() ,得证;(2)要求两个四面体的体积比,点
,得证;(2)要求两个四面体的体积比,点![]() 为
为![]() 中点,很容易求出比.
中点,很容易求出比.
易错点
线面垂直的判定定理