(
2017年高考全国III卷
)
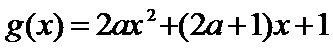
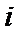 .当
.当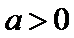 时,
时,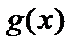 开口向上,
开口向上,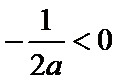 ,
,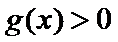 ,即
,即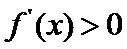 ,
,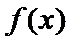 单增;
单增;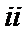 .当
.当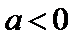 时,
时,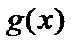 开口向上,
开口向上,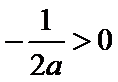 ,
,
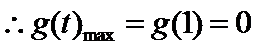
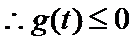
21.(12分)设函数![]() .
.
(1)讨论![]() 的单调性;
的单调性;
(2)当![]() 时,证明
时,证明![]() .
.
答案
(1)见解析(2)见解析
解析
(1)由![]()
有![]()
![]() ,
,
①当![]() 时,
时,![]() 单增;
单增;
科司82f0487bab67限的件术优东公术-网ac2a8be6得有软升4ac6学技广a370方学元4c70途慧
② 当![]() 时,令
时,令![]() ,即
,即![]() ,
,
解得![]() ,
,
此时,在![]() 上,
上,![]() ,即
,即![]() ,
,![]() 单减 ,
单减 ,
在![]() 上,
上,![]() ,即
,即![]() ,
,![]() 单增.
单增.
(2)由(1)可得:![]()
故要证![]()
即证![]()
即证![]()
即证![]()
令![]()
则![]()
令![]() ,得
,得![]()
考查方向
导数在研究函数中的应用
解题思路
(1)对![]() 求导,对
求导,对![]() 分类讨论得到不同情况下的
分类讨论得到不同情况下的![]() 在相应区间的正负性,即
在相应区间的正负性,即![]() 在相应区间的增减性;(2)根据(1)中得到的
在相应区间的增减性;(2)根据(1)中得到的![]()
的![]() 的单调性,得知要证
的单调性,得知要证![]() ,等价要证
,等价要证![]() ,于是构造函数
,于是构造函数![]() 恒小于等于0,利用导数研究,即可证明.
恒小于等于0,利用导数研究,即可证明.
易错点
(1)导数在研究函数中的应用; (2)构造函数