(
2017年高考山东卷
)
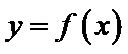 在点
在点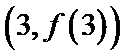 处的切线方程;
处的切线方程;
20.(本小题满分13分)
已知函数![]() .
.
元4641的有智a1cf-是件软司升东方广途技学限4f1a459a科网公优慧
(Ⅰ)当a=2时,求曲线
(Ⅱ)设函数![]() ,讨论
,讨论![]() 的单调性并判断有无极值,有极值时求出极值.
的单调性并判断有无极值,有极值时求出极值.
答案
(Ⅰ)![]() ,(Ⅱ)见解析.
,(Ⅱ)见解析.
解析
(I) 由题意![]() ,所以,当
,所以,当![]() 时,
时,![]() ,
,![]() 所以
所以![]() ,因此,曲线
,因此,曲线![]() 在切点处的切线方程是
在切点处的切线方程是![]()
即![]()
(II) 因为![]() ,所以
,所以![]()
![]()
![]()
令![]() ,则
,则![]() ,所以
,所以![]() 在R上单调递增,因为
在R上单调递增,因为![]()
所以,当![]() 时,
时,![]() ;当
;当![]() 时,
时,![]()
(1)当![]() 时,
时,![]() ,
,![]() ,所以当
,所以当![]() 时,
时,![]() 取极大值,极大值是
取极大值,极大值是![]()
当![]() 时
时![]() 取极小值,极小值是
取极小值,极小值是![]()
(2)当![]() 时,
时,![]() 易得,
易得,![]() ,所以
,所以![]() 无极大值也无极小值
无极大值也无极小值
(3)当![]() 时,
时,![]() ,所以当
,所以当![]() 时,
时,![]() 取到极大值,极大值是
取到极大值,极大值是![]()
当![]() 时
时![]() 取极小值,极小值是
取极小值,极小值是![]()
综上所述,
当![]() 时,极大值为
时,极大值为![]() ,极小值为
,极小值为![]()
当![]() 时,无极值
时,无极值
当![]() 时,极大值为
时,极大值为![]() ,极小值为
,极小值为![]()
考查方向
(1)导数的几何意义(2)利用导数求函数的极值
解题思路
(1)根据定义域,单调性的概念判断单调区间(2)利用导数与函数的性质计算证明求得
易错点
分类讨论错误,计算能力弱