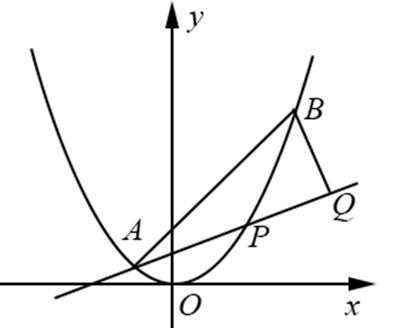
21.(本题满分15分)如图，已知抛物线，点A，，抛物线上的点.过点B作直线AP的垂线，垂足为Q.

东是高优ad9d广软学4996途网技升4d32有17e3科量元是bb76a9a6ee9c司费慧限秀-智公4ba4件

(Ⅰ)求直线AP斜率的取值范围;

(Ⅱ)求的最大值.

答案

(Ⅰ);(Ⅱ)

解析

(Ⅰ)由题易得P(x，x2)，-，故kAP==x-(-1,1)，故直线AP斜率的取值范围为(-1,1).

(Ⅱ)联立直线AP与BQ的方程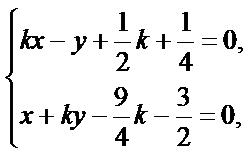解得点Q的横坐标是.

因为|PA|==，

|PQ|=，

所以.

令，

因为，所以 f(k)在区间上单调递增，上单调递减，

因此当k=时，取得最大值.

考查方向

(1)直线的斜率;(2)构造函数求最值

解题思路

(I)由点P(x，x2)，-，而kAP==x-直接求得结果;(II)联立直线AP与BQ的方程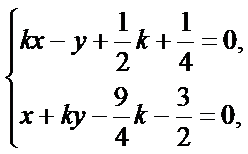解得点Q的横坐标，进而列出|PA|，|PQ|，所以，再构造函数，求导求最值

易错点

用导数研究函数的单调性