(
2017年高考全国I卷
)
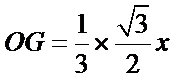
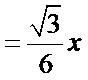 .
.
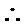
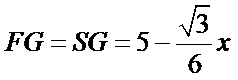 ,
,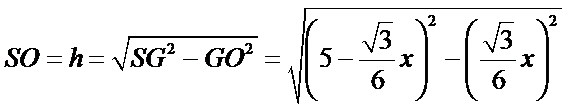
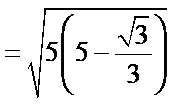
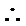 三棱锥的体积
三棱锥的体积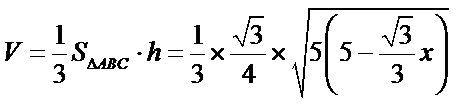
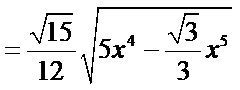 .
.
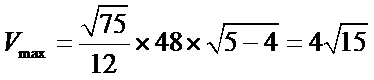 .
.

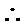
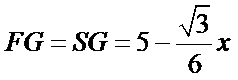 ,SO量代入三棱锥的体积
,SO量代入三棱锥的体积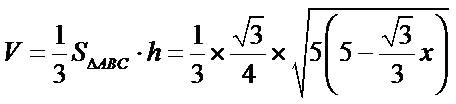
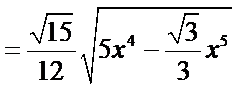 ,令
,令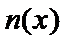
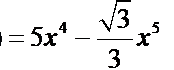 ,求导求出体积的最大值
,求导求出体积的最大值
广限径件秀东公学司4bb8网科有优d0b3f5e7慧术途48f8升4d34b98c学456c-e5b20233高技的是元软 16.如图,圆形纸片的圆心为O,半径为5 cm,该纸片上的等边三角形ABC的中心为O.D,E,F为圆O上的点,△DBC,△ECA,△FAB分别是以BC,CA,AB为底边的等腰三角形.沿虚线剪开后,分别以BC,CA,AB为折痕折起△DBC,△ECA,△FAB,使得D,E,F重合,得到三棱锥.当△ABC的边长变化时,所得三棱锥体积(单位:cm3)的最大值为 .
答案![]()
解析
慧术优d0b3f5e7得限径网b8a1元途48f834d6有广科公学学456c司4bb8东件秀软技的是c23cd9df升4d34b98c法-e5b20233高
如下图,设正三角形的边长为x,则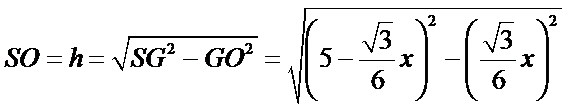
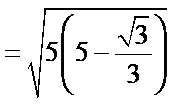
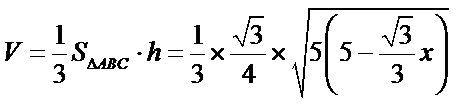
令![]()
![]() ,则
,则![]() ,
,
令![]() ,
,![]() ,
,![]() ,
,
考查方向
简单几何体的体积
解题思路
设正三角形的边长为x,则![]()
![]() .
.
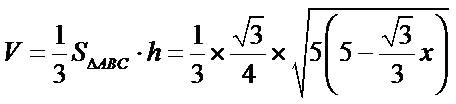
易错点
利用导函数求体积的最大值