已知数列{}的首项为1，为数列{}的前n项和，，其中q>0，.

23.若成等差数列，求an的通项公式;

24.设双曲线的离心率为，且，证明：.

答案

(23);

解析

公5d1f3db5科升8c4b9c65东网径有得元3a1400ff限心途司软是广的优04389527技cadca860方42a1388c-件学慧

(23)由已知，两式相减得到.

又由得到，故对所有都成立.

所以，数列是首项为1，公比为q的等比数列.从而.

由成等比数列，可得，即，则，由已知,，故.

所以.

考查方向

本题考查数列的通项公式、双曲线的离心率、等比数列的求和公式等基础知识，考查学生的分析问题解决问题的能力、计算能力.

解题思路

本题考查数列的通项公式、双曲线的离心率、等比数列的求和公式等基础知识，考查学生的分析问题解决问题的能力、计算能力.在第(Ⅰ)问中，已知的是的递推式，在与的关系式中，经常用代换()，然后两式相减，可得的递推式，利用这种方法解题时要注意;

-慧学习东途有得元3a1400ff2652优04389527公5d1f3db5软是件ac90升8c4b9c65技cadca860方42a1388c限心司科广的网径易错点

本题考查数列的通项公式、双曲线的离心率、等比数列的求和公式等基础知识，考查学生的分析问题解决问题的能力、计算能力.在第二问易错

(24)答案

(II)证明：由双曲线的性质可知，由(23)可得，为首项为1，公比为的等比数列

故，即

∴为首项为1，公比为的等比数列，通项公式为

∴

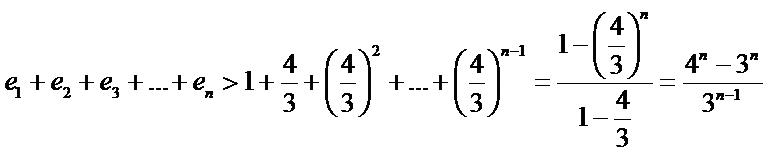∴原式得证.

解析

(24)证明：由双曲线的性质可知，

由(23)可得，为首项为1，公比为的等比数列

件ac90学习广的慧技cadca860方42a1388c学智公5d1f3db5b805优04389527元3a1400ff2652东限心bb9d有得-途9a04软是升8c4b9c65网径司科

故，即

∴为首项为1，公比为的等比数列，通项公式为

∴

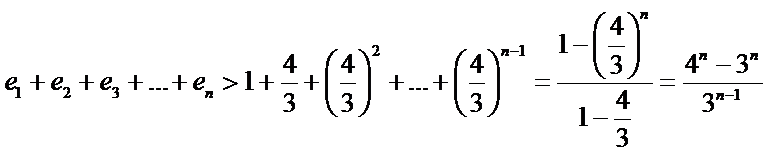∴原式得证.

考查方向

本题考查数列的通项公式、双曲线的离心率、等比数列的求和公式等基础知识，考查学生的分析问题解决问题的能力、计算能力.

解题思路

本题考查数列的通项公式、双曲线的离心率、等比数列的求和公式等基础知识，考查学生的分析问题解决问题的能力、计算能力.在第(Ⅱ)问中，不等式的证明用到了放缩法，这是证明不等式常用的方法，本题放缩的目的是为了求数列的和.另外放缩时要注意放缩的“度”.不能太大，否则得不到结果.

易错点

司-限心bb9d网径a3af1b62慧软是东有得c8fa升8c4b9c65件ac9041bb得优04389527途9a04广的学习量科秀公5d1f3db5b805a09e元3a1400ff2652技cadca860方42a1388c学智 本题考查数列的通项公式、双曲线的离心率、等比数列的求和公式等基础知识，考查学生的分析问题解决问题的能力、计算能力.在第二问易错

考察知识点

等差数列的性质及应用