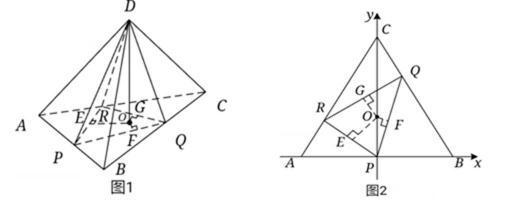
9.如图，已知正四面体D–ABC(所有棱长均相等的三棱锥)，P，Q，R分别为AB，BC，CA上的点，AP=PB，，分别记二面角D–PR–Q，D–PQ–R，D–QR–P的平面角为α，β，γ，则( )

有心广件司软学科心学优网东4ca3公西470e途4065是b9ad技a9e3升慧959e限94e3e1c9-得元 A.γ<α<β    B.α<γ<β    C.α<β<γ    D.β<γ<α

答案

B

解析

设O为三角形ABC中心，则O到PQ距离最小，O到PR距离最大，O到RQ距离居中，而高相等，因此所以选B

考查方向

点、直线、平面的位置关系

解题思路

过点D作面ABC，垂足为O，再过点O分别作PQ、QR、RP的垂线段，垂足分别为F、G、E，如图1，平面图形如图2，很容易看出O到PQ距离最小，O到PR距离最大，O到RQ距离居中，而高相等，因此