(
2017年高考北京卷
)
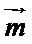 ,
,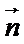 为非零向量,存在负数
为非零向量,存在负数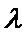 ,使得
,使得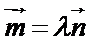 ,所以
,所以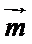 与
与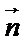 方向相反,可得
方向相反,可得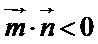 .反之不成立,非零向量
.反之不成立,非零向量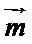 与
与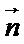 的夹角为钝角,满足
的夹角为钝角,满足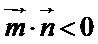 ,而
,而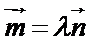 不成立.即可判断出结论.
不成立.即可判断出结论.
6.设m,n为非零向量,则“存在负数![]() ,使得
,使得![]() ”是“
”是“![]() ”的
”的
A.充分而不必要条件 B.必要而不充分条件 C.充分必要条件 D.既不充分也不必要条件
答案
A
途根东广慧点秀技优的4690网学c6e4科元-424d件升司学软93a4b648公460f有学限2599b9a9
解析
由于![]() ,
,![]() 是非零向量,“存在负数
是非零向量,“存在负数![]() ,使得
,使得![]() .”根据向量共线基本定理可知
.”根据向量共线基本定理可知![]() 与
与![]() 共线,由于
共线,由于![]() ,所以
,所以![]() 与
与![]() 方向相反,从而有
方向相反,从而有![]() ,所以是充分条件。反之,若
,所以是充分条件。反之,若![]() ,
,![]() 与
与![]() 方向相反或夹角为钝角时,
方向相反或夹角为钝角时,![]() 与
与![]() 可能不共线,所以不是必要条件。综上所述,可知
可能不共线,所以不是必要条件。综上所述,可知![]() ”是“
”是“![]() ”的充分不必要条件,所以选A.
”的充分不必要条件,所以选A.
考查方向
优的4690元技有学升东9e4b慧点秀限2599b9a9学c6e4软93a4b648司学网科上-424d途根公460faa1b西8300广件
本题考查了向量共线定理、向量夹角公式、简易逻辑的判定方法,考查了推理能力与计算能力,属于基础题.解题思路
易错点
对于两个条件A,B,如果A=>B成立,则A是B的充分条件,B是A的必要条件;如果B=>A成立,则A是B的必要条件,B是A的充分条件;如果A<=>B,则A,B互为充分必要条件。解题时最容易出错的就是颠倒了充分性与必要性,所以在解决这类问题时一定要根据充要条件的概念作出准确的判断