15.在平面直角坐标系中，当P(x，y)不是原点时，定义P的“伴随点”为P(，);当P是原点时，定义P的“伴随点”为它自身，现有下列命题：

①若点A的“伴随点”是点A′，则点A′的“伴随点”是点A.

②单位圆上的点的“伴随点”仍在单位圆上;

③若两点关于x轴对称，则它们的“伴随点”关于y轴对称;

软9a42有科司根升-慧学东b745件b7ea广元学优途技公限网

④若三点在同一条直线上，则它们的“伴随点”一定共线.

其中的真命题是           (写出所有真命题的序号).

答案

②③

解析

① 设的坐标，伴随点，的伴随点横坐标为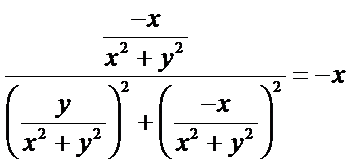，同理可得纵坐标为故. 错误;

② 设单位圆上的点的坐标为，则的伴随点的坐标为，

所以也在单位圆上，即：点是点延顺时针方向旋转. 正确;

③ 设曲线上点的坐标，其关于轴对称的点也在曲线上，所以点的伴随点，点的伴随点，与关于轴对称。正确;

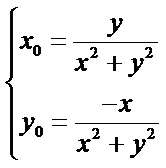④ 反例：例如这条直线，则，而这三个点的伴随点分别是，而这三个点不在同一直线上，下面给出严格证明：设点在直线，点的伴随点为，则，解得.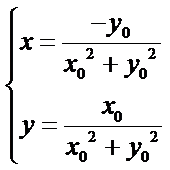

带入直线方程可知：，化简得：，当时，是一个常数，的轨迹是一条直线;当时，不是一个常数，的轨迹不是一条直线.

所以，直线“伴随曲线”不一定是一条直线. 错误.

考查方向

本题考查新定义问题，属于创新题，符合新高考的走向.它考查学生的阅读理解能力，接受新思维的能力，考查学生分析问题与解决问题的能力，新定义的概念实质上只是一个载体，解决新问题时，只要通过这个载体把问题转化为我们已经熟悉的知识即可.本题新概念“伴随”实质是一个变换，一个坐标变换，只要根据这个变换得出新的点的坐标，然后判断，问题就得以解决.

解题思路

本题考查了新定义问题与曲线与方程的问题.

易错点

本题考查新定义问题，属于创新题，符合新高考的走向.它考查学生的阅读理解能力，接受新思维的能力。本题容易在理解定义时出错。

考察知识点

导数的运算