如图，在四棱锥P-ABCD中，PA⊥CD，AD∥BC，∠ADC=∠PAB=90°，BC=CD=?AD。
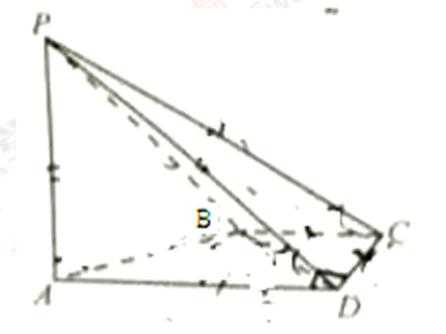
19.在平面PAD内找一点M，使得直线CM∥平面PAB，并说明理由;
20.证明：平面PAB⊥平面PBD。
19.答案
取棱AD的中点M，证明详见解析;
解析
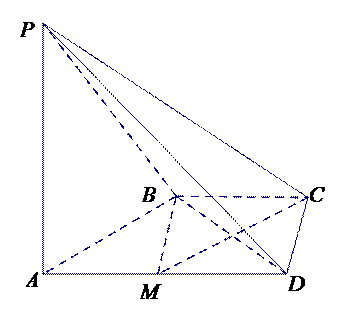
取棱AD的中点M(M∈平面PAD)，点M即为所求的一个点.理由如下：
因为AD‖BC,BC=
AD，所以BC‖AM, 且BC=AM.
所以四边形AMCB是平行四边形，从而CM‖AB.
又AB
平面PAB,CM
平面PAB,
所以CM∥平面PAB.
(说明：取棱PD的中点N,则所找的点可以是直线MN上任意一点)
考查方向
本题考查了线面平行、线线平行、线线垂直、线面垂直的问题
解题思路
本题考查线面平行、面面垂直的判断，考查空间想象能力、分析问题的能力、计算能力.证明线面平行时，可根据判定定理的条件在平面内找一条平行线，而这条平行线一般是由过面外的直线的一个平面与此平面相交而得，证明时注意定理的另外两个条件(线在面内，线在面外)要写全，否则会被扣分，求线面角(以及其他角)，证明面面垂直时，要证线面垂直，要善于从图形中观察有哪些线线垂直，从而可能有哪个线面垂直，确定要证哪个线线垂直，切忌不加思考，随便写.
易错点
本题考查线面平行、面面垂直的判断，考查空间想象能力、分析问题的能力、计算能力.证明线面平行时，容易在证明平行时步骤不全面出现错误。
20.答案由已知，PA⊥AB, PA ⊥ CD,
因为AD∥BC,BC=
AD，所以直线AB与CD相交，
所以PA ⊥平面ABCD.
从而PA ⊥ BD.
因为AD∥BC,BC=
AD，
所以BC∥MD,且BC=MD.
所以四边形BCDM是平行四边形.
所以BM=CD=
AD，所以BD⊥AB.
又AB∩AP=A,所以BD⊥平面PAB.
又BD
平面PBD,
所以平面PAB⊥平面PBD.
解析
由已知，PA⊥AB, PA ⊥ CD,
因为AD∥BC,BC=AD，所以直线AB与CD相交，
所以PA ⊥平面ABCD.
从而PA ⊥ BD.
因为AD∥BC,BC=AD，
所以BC∥MD,且BC=MD.
所以四边形BCDM是平行四边形.
所以BM=CD=AD，所以BD⊥AB.
又AB∩AP=A,所以BD⊥平面PAB.
又BD平面PBD,
所以平面PAB⊥平面PBD.
考查方向
本题考查了线面平行、线线平行、线线垂直、线面垂直的问题
解题思路
本题考查线面平行、面面垂直的判断，考查空间想象能力、分析问题的能力、计算能力.证明线面平行时，可根据判定定理的条件在平面内找一条平行线，而这条平行线一般是由过面外的直线的一个平面与此平面相交而得，证明时注意定理的另外两个条件(线在面内，线在面外)要写全，否则会被扣分，求线面角(以及其他角)，证明面面垂直时，要证线面垂直，要善于从图形中观察有哪些线线垂直，从而可能有哪个线面垂直，确定要证哪个线线垂直，切忌不加思考，随便写.
易错点
本题考查线面平行、面面垂直的判断，考查空间想象能力、分析问题的能力、计算能力.证明线面平行时，容易在证明平行时步骤不全面出现错误。
考察知识点
平行关系的综合应用