如图所示，倾角为α的斜面A被固定在水平面上，细线的一端固定于墙面，另一端跨过斜面顶端的小滑轮与物块B相连，B静止在斜面上.滑轮左侧的细线水平，右侧的细线与斜面平行.A、B的质量均为m.撤去固定A的装置后，A、B均做直线运动.不计一切摩擦，重力加速度为g.求：

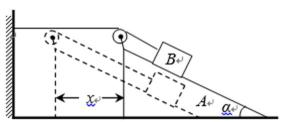
29.A固定不动时，A对B支持力的大小N;

30.A滑动的位移为x时，B的位移大小s;

31.A滑动的位移为x时的速度大小v_x.

(1)答案

支持力的大小 N = mgcosα

解析

根据受力分析：重力、支持力与绳子的拉力，结合力的平行四边形定则，及平衡条件与三角知识，则斜面的支持力大小为：N=mgcosα;

考查方向

受力分析

解题思路

依据力的合成法则，结合平衡条件与三角知识，即可求解;

易错点

力的分解的表达式

(2)答案

s=x;

解析

撤去固定A的装置后，A、B均做直线运动，根据运动的合成与分解，当A滑动的位移为x时，设B的位移大小s，根据几何关系s_x = x(1 – cosα)，s_y = xsinα，且s² = sx² + sy²

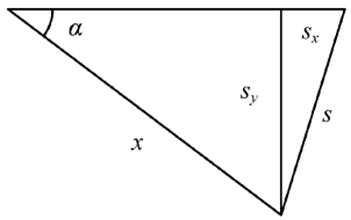
解得s =?x

考查方向

牛顿运动定律的综合应用

解题思路

根据运动的合成与分解，结合各自位移存在的几何关系，及三角知识，即可求解;

易错点

掌握运动的合成与分解与三角知识的内容

(3)答案

vA=

解析

因B的下降的高度为s_y=xsinα;

根据系统只有重力做功，机械能守恒定律，则有：

mgs_y=+

如下图所示，画阴影部分的三角形相似，依据位移之比等于速度之比，

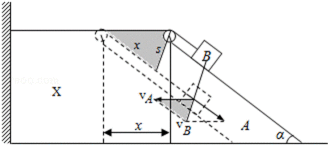
可得：=

则有：v_B=v_A;

解得：v_A=

考查方向

匀变速直线运动规律的综合运用

解题思路

根据系统只有重力做功，机械能守恒，结合相似三角形，得出速度之比等于位移之比，从而求解.

易错点

确定位移之比与速度之比是解题的关键

考察知识点

共点力平衡的条件及其应用