已知椭圆E:的一个焦点与短轴的两个端点是正三角形的三个顶点,点
在椭圆E上。
(1).求椭圆E的方程;
(2).设不过原点O且斜率为的直线l与椭圆E交于不同的两点A,B,线段AB的中点为M,直线OM与椭圆E交于C,D,证明:︳MA︳·︳MB︳=︳MC︳·︳MD︳
(1)答案
解析
(1)由已知,a=2b.
又椭圆![]() 过点
过点![]() ,故
,故
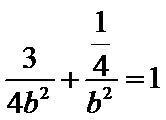 ,解得
,解得
所以椭圆E的方程是![]() .
.
考查方向
本题考查椭圆的标准方程及其几何性质,考查学生的分析问题解决问题的能力和数形结合的思想.在涉及到直线与椭圆(圆锥曲线)的交点问题时,一般都设交点坐标为,同时把直线方程与椭圆方程联立,消元后,可得,再把用表示出来,并代入刚才的,这种方法是解析几何中的“设而不求”法.可减少计算量,简化解题过程
解题思路
由椭圆两个焦点与短轴的一个端点是正三角形的三个顶点可得![]() ,椭圆的标准方程中可减少一个参数,再利用
,椭圆的标准方程中可减少一个参数,再利用![]() 在椭圆上,可解出b的值,从而得到椭圆的标准方程;
在椭圆上,可解出b的值,从而得到椭圆的标准方程;
易错点
本题考查椭圆的标准方程及其几何性质,考查学生的分析问题解决问题的能力和数形结合的思想.在涉及到直线与椭圆(圆锥曲线)的交点问题,联立化简易出错。
(2)答案
设直线![]() 的方程为
的方程为![]() ,
,
由方程组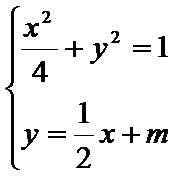 得
得![]()
判别式为![]() ,由
,由![]() ,即
,即![]() ,解得
,解得![]()
由根与系数的关系可得![]()
所以![]() 点的坐标为
点的坐标为![]() ,直线
,直线![]() 的方程为
的方程为![]()
联立可得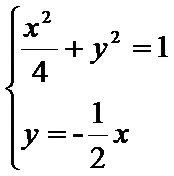 得
得![]() 、
、![]()
所以![]() .
.
又![]()
所以![]() .
.
解析
(2)设直线![]() 的方程为
的方程为![]() ,
,![]()
由方程组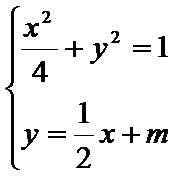 得
得![]()
判别式为![]() ,由
,由![]() ,即
,即![]() ,解得
,解得![]()
由根与系数的关系可得![]()
所以![]() 点的坐标为
点的坐标为![]() ,直线
,直线![]() 的方程为
的方程为![]()
联立可得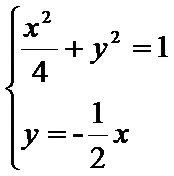 得
得![]() 、
、![]()
所以![]() .
.
又![]()
所以![]() .
.
考查方向
本题考查椭圆的标准方程及其几何性质,考查学生的分析问题解决问题的能力和数形结合的思想.在涉及到直线与椭圆(圆锥曲线)的交点问题时,一般都设交点坐标为,同时把直线方程与椭圆方程联立,消元后,可得,再把用表示出来,并代入刚才的,这种方法是解析几何中的“设而不求”法.可减少计算量,简化解题过程
解题思路
(2)首先设出直线![]() 方程为
方程为![]() ,同时设交点
,同时设交点![]() ,把
,把![]() 方程与椭圆方程联立后消去
方程与椭圆方程联立后消去![]() 得
得![]() 的二次方程,利用根与系数关系,得
的二次方程,利用根与系数关系,得![]() ,由
,由![]()
![]() 求得
求得![]() (用
(用![]() 表示),由
表示),由![]() 方程
方程![]() 具体地得出
具体地得出![]() 坐标,也可计算出
坐标,也可计算出
易错点
本题考查椭圆的标准方程及其几何性质,考查学生的分析问题解决问题的能力和数形结合的思想.在涉及到直线与椭圆(圆锥曲线)的交点问题,联立化简易出错。
考察知识点
椭圆的定义及标准方程