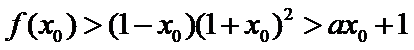21.(12分)

设函数.

(1)讨论的单调性;

公网途-高软元学司有a6b5优限科慧4d36c4e8技东广件智升 (2)当时，，求的取值范围.

答案

(1)见解析 (2)[1，+∞)

解析

(1)f ’(x)=(1-2x-x²)e^x

令f’(x)=0得x=-1-，x=-1+

当x∈(-∞，-1-)时，f’(x)<0;当x∈(-1-，-1+)时，f’(x)>0;当x∈(-1-，+∞)时，f’(x)<0

所以f(x)在(-∞，-1-)，(-1+，+∞)单调递减，在(-1-，-1+)单调递增

(2) f (x)=(1+x)(1-x)e^x

当a≥1时，设函数h(x)=(1-x)e^x，h’(x)= -xe^x<0(x>0)，因此h(x)在[0，+∞)单调递减，而h(0)=1，

故h(x)≤1，所以

f(x)=(x+1)h(x)≤x+1≤ax+1

当0＜a＜1时，设函数g（x）=ex-x-1，g’（x）=ex-1＞0(x>0)，所以g(x)在在[0，+∞)单调递增，而g(0)=0，故e^x≥x+1

当0＜x＜1，，，取

则

当

综上，a的取值范围[1，+∞)

考查方向

(1)利用导数研究函数的单调性;(2)利用导数求参数的取值范围

解题思路

(1)先求函数导数，再求导函数零点，列表分析导函数符号确定单调区间(2)对分类讨论，当a≥1时，，满足条件;当时，取，当

0＜a＜1，

易错点

利用导数研究不等式恒成立问题