(
2016年高考浙江卷
)

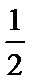
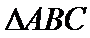 中,因为
中,因为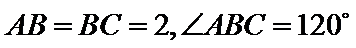 ,所以
,所以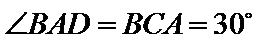 .
.


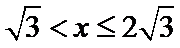 时,有
时,有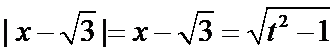 ,故
,故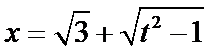 .
.
14.如图,在![]() 中,AB=BC=2,
中,AB=BC=2,![]() .若平面ABC外的点P和线段AC上的点D,满足PD=DA,PB=BA,则四面体PBCD的体积的最大值是 .
.若平面ABC外的点P和线段AC上的点D,满足PD=DA,PB=BA,则四面体PBCD的体积的最大值是 .
答案
有法途54f4科4ee7限a257慧网升件元司公软技东学智-秀广优
解析
由余弦定理可得![]()
![]() ,所以
,所以![]() .
.
设![]() ,则
,则![]() ,
,![]() .
.
在![]() 中,由余弦定理可得
中,由余弦定理可得![]()
![]()
![]() .
.
故![]() .
.
在![]() 中,
中,![]() ,
,![]() .
.
由余弦定理可得![]() ,所以
,所以![]() .
.
过![]() 作直线
作直线![]() 的垂线,垂足为
的垂线,垂足为![]() ,设
,设![]() 则
则![]() ,即
,即![]() ,解得
,解得![]() .
.
而![]() 的面积
的面积![]() .
.
设![]() 与平面
与平面![]() 所成角为
所成角为![]() ,则点
,则点![]() 到平面
到平面![]() 的距离
的距离![]() .
.
故四面体![]() 的体积
的体积![]()
![]()
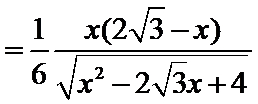 .
.
设![]() ,因为
,因为![]() ,所以
,所以![]() .,则
.,则![]() .
.

广4d87386ff24d东司上法-秀心4e81409f有法网智点优径学智根科4ee71672软88f889e0根途54f46c431cb0a763件慧4c56公ffffa44d限a25749d5费技秀元升
(2)当
此时,![]()
![]() .
.
由(1)可知,函数![]() 在
在![]() 单调递减,故
单调递减,故![]() .
.
综上,四面体![]() 的体积的最大值为
的体积的最大值为![]() .
.
考查方向
立体几何中的变化问题
解题思路
设![]() ,将体积写成关于
,将体积写成关于![]() 的函数,再求最值
的函数,再求最值
易错点
体积无法写成关于![]() 的函数,求函数最大值有困难。
的函数,求函数最大值有困难。
考察知识点
直线、平面垂直的综合应用