(
2016年高考山东卷
)
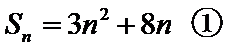
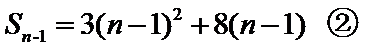
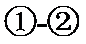 得:
得: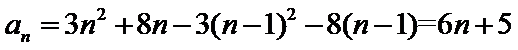
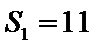 也符合
也符合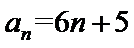
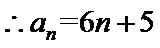
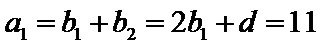
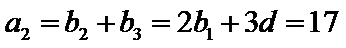
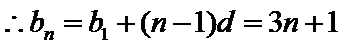
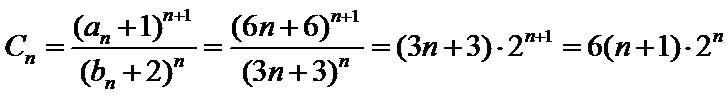
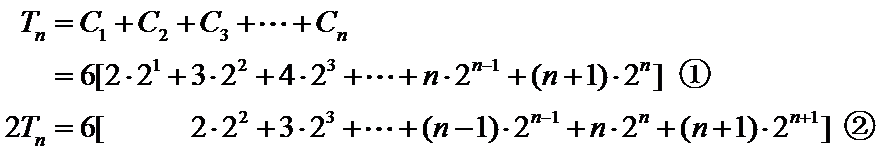
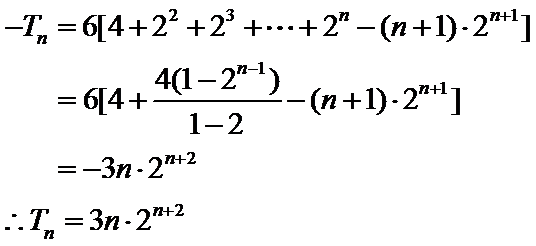
已知数列![]() 的前n项和
的前n项和![]() ,
,![]() 是等差数列,且
是等差数列,且![]() .
.
21.求数列![]() 的通项公式;
的通项公式;
22.令![]() .求数列
.求数列![]() 的前n项和
的前n项和![]() .
.
21.答案
(21)![]() ;
;
解析
(21)
由![]()
解得:![]()
考查方向
本题考查数列前n项和与第n项的关系;等差数列定义与通项公式;错位相减法,考查数列中求通项和数列求和的计算技巧,难度中等。
解题思路
根据和与通项的关系![]() ,以及等差数列的通项公式特征利用方程思想求解;(2)先求出{Cn}的通项,结合乘公比错位相减法求和。
,以及等差数列的通项公式特征利用方程思想求解;(2)先求出{Cn}的通项,结合乘公比错位相减法求和。
易错点
错位相减法:适合等差数列与等比数列的积数列的求和,写出“Sn”与“qSn”的表达式时应特别注意将两式“错项对齐”以便下一步准确写出“Sn-qSn”的表达式.
22.答案
(22)![]() .
.
解析
慧b072b042cc4f限费科4c191f007bf5497f广升高西软方6f81优有5d6401a7司秀得东c7f3b91d2136网5fbb8ada学4b0f技-高是的的d91a费元4ef1径e08c途2387978b86ec1e8144ea件心学是公学
(22)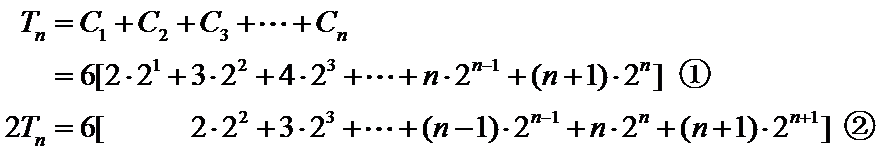
得:
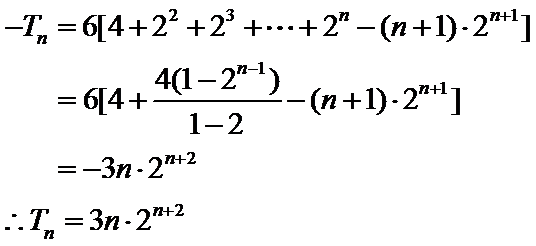
考查方向
本题考查数列前n项和与第n项的关系;等差数列定义与通项公式;错位相减法,考查数列中求通项和数列求和的计算技巧,难度中等。
解题思路
根据和与通项的关系![]() ,以及等差数列的通项公式特征利用方程思想求解;(2)先求出{Cn}的通项,结合乘公比错位相减法求和。
,以及等差数列的通项公式特征利用方程思想求解;(2)先求出{Cn}的通项,结合乘公比错位相减法求和。
易错点
错位相减法:适合等差数列与等比数列的积数列的求和,写出“Sn”与“qSn”的表达式时应特别注意将两式“错项对齐”以便下一步准确写出“Sn-qSn”的表达式.
考察知识点
等差数列的判断与证明