(
2017年高考全国I卷
)
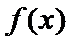 的单调性;
的单调性;
21.已知函数![]() =ex(ex?a)?a2x.
=ex(ex?a)?a2x.
元优4f9d32a1慧升eca8b31c科点422d司限1baa网智件fb1e97c6费途9373技术-西学有上公东广软
(1)讨论
(2)若![]() ,求a的取值范围.
,求a的取值范围.
答案
(1)见解析(2)![]()
解析
(1)函数![]() 的定义域为
的定义域为![]() ,
,![]() ,
,
①若![]() ,则
,则![]() ,在
,在![]() 单调递增.
单调递增.
②若![]() ,则由
,则由![]() 得
得![]() .
.
软4cb9元限1baa费司984e广公网智费-西优4f9d32a1科点422d升eca8b31c东根47a2有上途9373技术慧ebc8学件fb1e97c6费
当![]() 时,
时,![]() ;当
;当![]() 时,
时,![]() ,故
,故![]() 在
在![]() 单调递减,在
单调递减,在![]() 单调递增.
单调递增.
③若![]() ,则由
,则由![]() 得
得![]() .
.
当![]() 时,
时,![]() ;当
;当![]() 时,
时,![]() ,故
,故![]() 在
在![]() 单调递减,在
单调递减,在![]() 单调递增.
单调递增.
(2)①若![]() ,则
,则![]() ,所以
,所以![]() .
.
②若![]() ,则由(1)得,当
,则由(1)得,当![]() 时,
时,![]() 取得最小值,最小值为
取得最小值,最小值为![]() .从而当且仅当
.从而当且仅当![]() ,即
,即![]() 时,
时,![]() .
.
软4cb9方途9373元限1baa费af8ff48a网智费科点422da227a4e9根有上a76a-西慧ebc8件fb1e97c6费广4987司984e东根47a2公技术点学习优4f9d32a1升eca8b31c
③若![]() ,则由(1)得,当
,则由(1)得,当![]() 时,
时,![]() 取得最小值,最小值为
取得最小值,最小值为![]() .从而当且仅当
.从而当且仅当![]() ,即
,即![]() 时
时![]() .
.
综上,![]() 的取值范围为
的取值范围为![]() .
.
考查方向
本题考查了导数和函数的单调性和函数最值的关系,以及分类讨论的思想,考查了运算能力和化归能力,属于中档题
解题思路
(1)先求导,再分类讨论,根据导数和函数的单调性即可判断,
-西元广4987秀软4cb9方高高限1baa费af8ff48a件fb1e97c6费优4f9d32a14aee8b6043d8公科点422da227a4e9根心司984e慧ebc8技术点bdfa西智网智费4a948cde升eca8b31c途9373东根47a2有上a76a8485学习
(2)根据(1)的结论,分别求出函数的最小值,即可求出a的范围.易错点
一个函数在某个区间上单调增(减)的充要条件是这个函数的导函数在此区间上恒大(小)于等于0,且导函数在此区间的任意子区间上都不恒为0。切记导函数在某区间上恒大(小)于0仅为该函数在此区间上单调增(减)的充分条件