设函数
，
，其中
（I）求
的单调区间;
（II）若
存在极值点
，且
，其中
，求证：
;
（III）设
，函数
，求证：
在区间
上的最大值不小于
.
(Ⅰ)答案
(Ⅰ)递减区间为
，递增区间为
，
.
解析
本题主要考察了导数的运算，利用导数研究函数的性质、证明不等式等知识点，属于拔高题，不容易得分，解析如下：
试题解析：(1)解：由
，可得
，下面分两种情况讨论：
①当
时，有
恒成立，所以
的单调增区间为
.
②当
时，令
，解得
或
.
当
变化时，
、
的变化情况如下表：
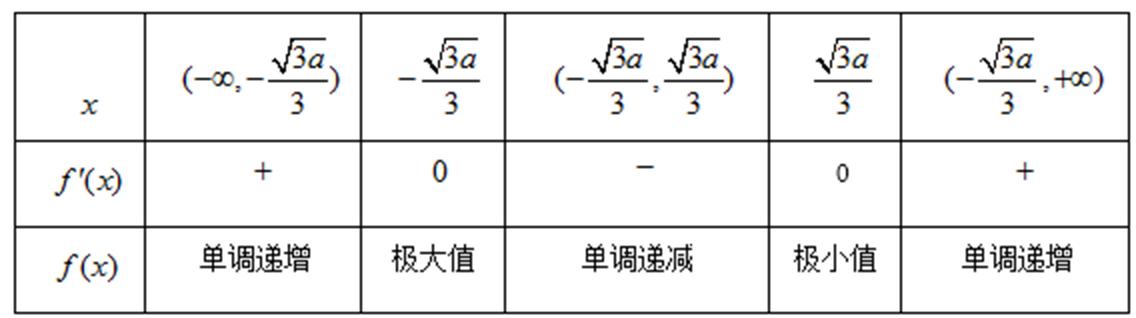
所以
的单调递减区间为
，单调递增区间为
，
.
考查方向
本题考查了导数的运算，利用导数研究函数的性质、证明不等式等知识点。
解题思路
(Ⅰ)先求函数的导数：
，再根据导函数零点是否存在情况，分类讨论：①当
时，有
恒成立，所以
的单调增区间为
.②当
时，存在三个单调区间
学西475a件途4894限优有ad13东科司升-慧8df6公广西术软元网技
易错点
第二问不知如何就参数的范围进行讨论导致失分。
(Ⅱ)答案
(Ⅱ)证明：因为
存在极值点，所以由(1)知
且
.
由题意得
，即
，
进而
，
又
，且
，
由题意及(1)知，存在唯一实数
满足
，且
，因此
，
所以
.
解析
本题主要考察了导数的运算，利用导数研究函数的性质、证明不等式等知识点，属于拔高题，不容易得分.
考查方向
本题考查了导数的运算，利用导数研究函数的性质、证明不等式等知识点。
解题思路
(Ⅱ)由题意得
即
，再由
化简可得结论
易错点
第二问不知如何就参数的范围进行讨论导致失分。
(III)答案
(3)证明：设
在区间
上的最大值为
，
表示
，
两数的最大值，下面分三种情况讨论：
①当
时，
，由(1) 知
在区间
上单调递减，
网科方54ab有ad13-优方东学升慧8df6be44根技73a3件秀广西术软的学西475a公术限4399de54a72d62b0司元途4894
所以
在区间
上的取值范围为
，因此，
所以
.
②当
时，
，
由(1)和(2) 知
，
，
所以
在区间
上的取值范围为
，
所以
③当
时，
，由(1)和(2)知，
，
，所以
在区间
上的取值范围为
，因此
。
综上所述，当
时，
在区间
上的最大值不小于
.
解析
本题主要考察了导数的运算，利用导数研究函数的性质、证明不等式等知识点，属于拔高题，不容易得分.
考查方向
本题考查了导数的运算，利用导数研究函数的性质、证明不等式等知识点。
解题思路
(Ⅲ)实质研究函数
最大值：主要比较
，
的大小即可，分三种情况研究①当
时，
，②当
时，
，③当
时，
.
易错点
第二问不知如何就参数的范围进行讨论导致失分。