（ 2016年高考山东卷 ）

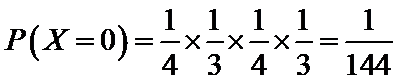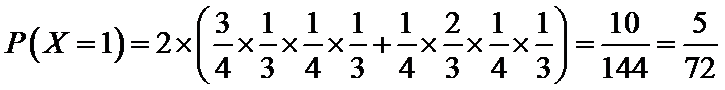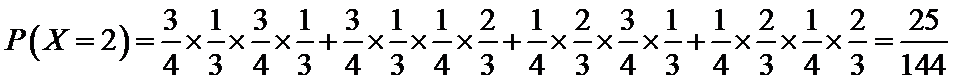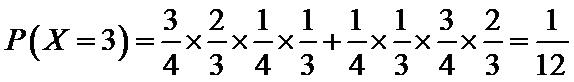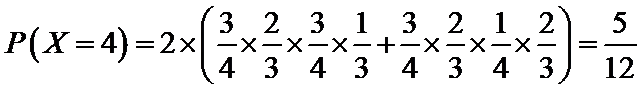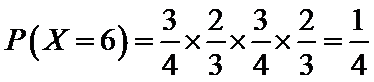甲、乙两人组成“星队”参加猜成语活动，每轮活动由甲、乙各猜一个成语，在一轮活动中，如果两人都猜对，则“星队”得3分;如果只有一个人猜对，则“星队”得1分;如果两人都没猜对，则“星队”得0分。已知甲每轮猜对的概率是，乙每轮猜对的概率是;每轮活动中甲、乙猜对与否互不影响。各轮结果亦互不影响。假设“星队”参加两轮活动，求：

(I).“星队”至少猜对3个成语的概率;

件-软公8aca优东科59f3广元术司法升途限学慧网有技 (II).“星队”两轮得分之和为X的分布列和数学期望EX

答案

(Ⅰ)

解析

(Ⅰ)记事件A:“甲第一轮猜对”，记事件B：“乙第一轮猜对”，

记事件C：“甲第二轮猜对”，记事件D：“乙第二轮猜对”，

记事件E：“‘星队’至少猜对3个成语”.

由题意，

由事件的独立性与互斥性，

所以“星队”至少猜对3个成语的概率为.

考查方向

本题考查独立事件的概率公式和互斥事件的概率加法公式;分布列和期望，推理与归纳能力，分类讨论思想，难度中等。

解题思路

由独立事件的概率公式和互斥事件的概率加法公式求解;

Ⅱ)

，

解析

(Ⅱ)由题意，随机变量X的可能取值为0,1,2,3,4,6.

由事件的独立性与互斥性，得

,
,,
,
,
，

可得随机变量X的分布列为

所以数学期望.

考查方向

本题考查独立事件的概率公式和互斥事件的概率加法公式;分布列和期望，推理与归纳能力，分类讨论思想，难度中等。

解题思路

由事件的独立性与互斥性，得到X的分布列，根据期望公式求解。