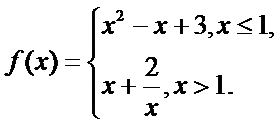8.已知函数设，若关于x的不等式在R上恒成立，则a的取值范围是( )

A      B       C      D

答案

A

解析

当时，关于x的不等式在R上恒成立，

即为

即有

由的对称轴为，可得处取得最大值

由的对称轴为，可得处取得最小值，

则①

当x>1时，关于x的不等式在R上恒成立，

即为，

即有

由(当且仅当)取得最大值;

由(当且仅当x=2>1)取得最小值2.

则②

由①②可得，

综上.故选A.

考查方向

本题考查分段函数的运用，不等式恒成立问题的解法，注意运用分类讨论和分离参数法，以及转化思想的运用，分别求出二次函数和基本不等式求最值是解题的关键，属于中档题.

解题思路

讨论当x≤1时，运用绝对值不等式的解法和分离参数，可，再由二次函数的最值求法，可得a的范围;讨论当x>1时，同样可得再由基本不等式可得最值，可得a的范围，求交集即可得到所求范围.

易错点

与分段函数相关的问题有作图、求值、求值域、解方程、解不等式、研究单调性及讨论奇偶性等等。在解决此类问题时，要注意分段函数是一个函数而不是几个函数，如果自变量取值不能确定，要对自变量取值进行分类讨论，同时还要关注分界点附近函数值变化情况。