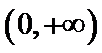
已知函数.

26.讨论的单调性;

27.若有两个零点,求的取值范围.

(I)答案

见解析

解析

(I)

(i)设,则当时,;当时,.

所以在单调递减,在单调递增.

(ii)设,由得x=1或x=ln(-2a).

①若,则,所以在单调递增.

②若,则ln(-2a)<1,故当时,;

当时,,所以在单调递增,在单调递减.

③若,则,故当时,,当时,,所以在单调递增,在单调递减.

考查方向

函数单调性,导数应用

解题思路

(I)先求得再根据1,0,2a的大小进行分类确定的单调性;

易错点

分类讨论思想及分类讨论原则、合理构造新函数.

(II)(i)设,则由(I)知,在单调递减,在单调递增.

又,取b满足b<0且,

则,所以有两个零点.

(ii)设a=0,则所以有一个零点.

(iii)设a<0,若,则由(I)知,在单调递增.

又当时,<0,故不存在两个零点;若,则由(I)知,在单调递减,在单调递增.又当时<0,故不存在两个零点.

综上,a的取值范围为.

考查方向

函数单调性,导数应用

解题思路

(II)借助第一问的结论,通过分类讨论函数单调性,确定零点个数,从而可得a的取值范围为

易错点

分类讨论思想及分类讨论原则、合理构造新函数.

考察知识点

导数的加法与减法法则