(
2017年高考山东卷
)
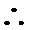 当
当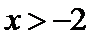 时,
时,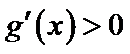 ,当
,当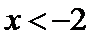 时,
时,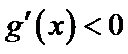 ,
,
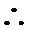
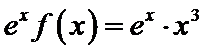 在
在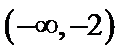 上单调递减,在
上单调递减,在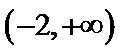 上单调递增,故
上单调递增,故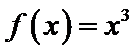 不具有
不具有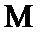 性质;
性质;
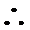
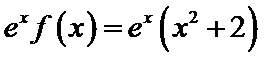 在
在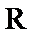 上单调递增,故
上单调递增,故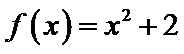 具有
具有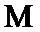 性质.
性质.
15.若函数![]() (
(![]() 是自然对数的底数)在
是自然对数的底数)在![]() 的定义域上单调递增,则称函数
的定义域上单调递增,则称函数![]() 具有
具有![]() 性质.下列函数中所有具有
性质.下列函数中所有具有![]() 性质的函数的序号为 .
性质的函数的序号为 .
①![]() ②
②![]() ③
③![]() ④
④![]()
答案
①④
解析
①![]() 在
在![]() 上单调递增,故
上单调递增,故![]() 具有
具有![]() 性质;
性质;
②![]() 在
在![]() 上单调递减,故
上单调递减,故![]() 不具有
不具有![]() 性质;
性质;
③![]() ,令
,令![]() ,则
,则![]() ,
,
④![]() ,令
,令![]() ,则
,则![]() ,
,
考查方向
(1)新定义问题;(2)利用导数研究函数的单调性.
解题思路
创新题,利用题中所给新定义的概念依次对①、②、③、④个选项分析转化成熟悉的知识进而得出结果.
易错点
创新题中新定义的理解与转化